Стороны многоугольника имеющие общую вершину. Многоугольники и их свойства. Соблюдение вашей конфиденциальности на уровне компании

Вершинами многоугольника, а отрезки сторонами многоугольника. Вершины многоугольника - страница №1/1

Геометрия 8 класс К.К.Кургинян Часть-1* (со звездочкой).
Многоугольник.

Определение: Многоугольник - это геометрическая фигура, которая состоит из плоской, замкнутой ломаной без самопересечений. Вершины ломаной называются вершинами многоугольника, а отрезки - сторонами многоугольника.

Вершины многоугольника называются соседними , если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями .

Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°. Сумма внешних углов многоугольника 360°.

Выпуклый многоугольник.
Многоугольник называется выпуклым если:
Определение I - для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём.

Определение II - каждый внутренний угол меньше 180° .

Определение III - все его диагонали полностью лежат внутри него.

Определение IV – он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов n -угольника.
Сумма углов выпуклого n-угольника равна (n-2)∙180°.
Сумма углов невыпуклого n-угольника также равна (n-2)∙180°. (Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники).
Число диагоналей n -угольника.*

Теорема: Число диагоналей всякого n-угольника равно n(n-3)2.

Доказательство: Пусть n - число вершин многоугольника, вычислим p- число возможных разных диагоналей. Каждая вершина соединена диагоналями со всеми другими вершинами, кроме двух соседних и, естественно, себя самой. Таким образом, из одной вершины можно провести n-3 диагонали; перемножим это на число вершин (n-3)∙n, однако, мы посчитали каждую диагональ дважды (по разу для каждого конца, следовательно, надо разделить на 2) - отсюда, p= n(n-3)2.

Задача*: в каком выпуклом многоугольнике диагоналей на 25 больше чем сторон?

25+n = nn-32

50 + 2n = n 2 - 3n

n 2 - 5n - 50 = 0

Разложим на множители

n 2 -25-5n -25 = 0

n=-5 не удовлетворяет,

так как не существует

такой многоугольник

n = 10 удовлетворяет

Ответ: Десяти угольник.

Фигуры с равными диагоналями.*

На плоскости существует два правильных многоугольника, у которых все диагонали равны между собой - это квадрат и правильный пятиугольник (пентагон) . У квадрата две одинаковых диагонали, пересекающихся в центре под прямым углом. У правильного пятиугольника пять одинаковых диагоналей, которые вместе образуют рисунок пятиконечной звезды (пентаграммы).

В пространстве существует единственный правильный многогранник (не многоугольник ), у которого все диагонали равны между собой - это правильный восьмигранник (октаэдр) . У октаэдра три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра - пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).

Помимо октаэдра есть еще один правильный многогранник, у которого все пространственные диагонали равны между собой - это куб (гексаэдр), помимо пространственных у куба есть диагонали граней . У куба четыре одинаковых пространственных диагонали, которые пересекаются в центре. Угол между диагоналями куба составляет либо arccos (1/3) ≈ 70,5° (для пары диагоналей, проведенных к смежным вершинам), либо arccos (–1/3) ≈ 109,5° (для пары диагоналей, проведенных к несмежным вершинам).

Четырехугольники.
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.

Две несмежные стороны называются противоположными.

Две не соседние вершины называются противоположными.
1.Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1) Противоположные стороны параллелограмма равны. AB=DC, AD=BC.

2) Противоположные углы параллелограмма равны. A=C, B=D.

3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD.

4) Сумма углов, прилежащих к одной стороне, равна 180°. A+D=180, A+B=180, B+C=180, D+C=180.

5) Сумма всех углов равна 360°. A+B+C+D=360°.

6)* Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: AC 2 +BD 2 =2∙(AB 2 +AD 2).

Задача 1*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна AC=9 см, а стороны AD=7 см и AB=4 см.

Решение: Подставив значения в формулу получим:

81+BD 2 =2∙(49+16),

BD 2 =49, следовательно вторая диагональ равна BD=7 см. Ответ: 7 см.
Задача 2*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна BD=10 см, а стороны AD=8 см и AB=2 см.

Решение: Условия задачи не верно, так как сумма двух сторон треугольника всегда больше третей стороны. Ответ: задача не имеет решений (смысла).

Задача 3*: а)Найти сторону параллелограмма, если известно, что длина диагоналей равна BD=6 см, AC=8, а одна сторона AB=5 см. б)Как называется этот параллелограмм.
Задача 4**: Сумма длин диагоналей параллелограмма равна 12 см, а произведение 32 найдите значение суммы квадратов всех его сторон.
Задача 5**: Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.

Решение: Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб .

Действительно, пусть a и b – длины соседних сторон параллелограмма, а и – длины его диагоналей (см. рис. 2). Тогда периметр параллелограмма: P = 2(a + b ).

Из равенства, выражающего теорему о сумме квадратов диагоналей параллелограмма, следует, что у всех параллелограммов с данными диагоналями сумма квадратов сторон есть величина постоянная.

По неравенству между средним арифметическим и средним квадратичным:  , причем равенство достигается т. и т. т., когда a = b . Значит, параллелограмм с наибольшим периметром является ромбом. Находим сторону этого ромба: =5(см). Ответ: 20 см.

2.Прямоугольник - это параллелограмм, у которого все углы прямые.
Определение 2: это четырёхугольник, у которого все углы прямые.

Определение 3: это параллелограмм, у которого один угол прямой.

Определение 4: это параллелограмм, у которого углы равны.
Свойства прямоугольника: +
1) Диагонали прямоугольника равны.

2)* Квадрат диагонали равен сумме квадратов сторон. AC 2 =AB 2 +DC 2

Задача 1: Меньшая сторона прямоугольника равна 5см, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
Задача 2: Меньшая сторона прямоугольника равна 24, диагонали пересекаются под углом 120°. Найдите диагонали и большую сторону прямоугольника.
Задача 3*: Сторона прямоугольника равна 3 см, диагональ 5 см. Найдите другую сторону прямоугольника.
Задача 4*: Сторона прямоугольника равна 6 см, диагональ 10 см. Найдите площадь прямоугольника.

3.Ромб - это параллелограмм, у которого все стороны равны.
Определение 2: это четырёхугольник, у которого все стороны равны.
Свойства ромба: те же свойства, что и у параллелограмма +
1) Диагонали ромба взаимно перпендикулярны (AC ⊥ BD).

2) Диагонали ромба делят его углы пополам (то есть диагонали ромба являются биссектрисами его углов- ∠DCA = ∠BCA, ∠ABD = ∠CBD, ∠BAC = ∠DAC, ∠ADB = ∠CDB).

3)*Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма). AC 2 +BD 2 =4·AB 2
Задача 1: Диагонали ромба 6 и 8 см. Найти сторону ромба.
Задача 2: Сторона ромба 10 см, один из углов 60. Найти маленькую диагональ ромба.
4.Квадрат -это параллелограмм, у которого все углы равны 90 и все стороны равны.
Определение 2: это параллелограмм, у которого все углы и стороны равны между собой.

Определение 3: это четырёхугольник, у которого все углы и стороны равны между собой.

Определение 4: это ромб, у которого один угол прямой.

Определение 5: это ромб, у которого углы равны.

Определение 6: это прямоугольник, у которого все стороны равны.
Свойства квадрата: те же свойства, что и у параллелограмма +
1) Диагонали квадрата равны.

2) Диагонали квадрата взаимно перпендикулярны (AC ⊥ BD).

3) Диагонали квадрата делят его углы пополам (то есть диагонали квадрата являются биссектрисами его углов- ∠DCA = ∠BCA= ∠ABD = ∠CBD= ∠BAC = ∠DAC= ∠ADB = ∠CDB=45).

4)* Квадрат диагонали равен удвоенному квадрату стороны. AC 2 =2·AB 2

5.Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны называются основаниями, а две другие боковыми.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Трапеция называется прямоугольной, если один из его углов прямой.
Задача: Докажите, что трапеция не может одновременно быть и прямоугольной и равнобедренной.

Многоугольник. Вершины, углы, стороны и диагонали
многоугольника. Периметр многоугольника.
Простой многоугольник. Выпуклый многоугольник.
Сумма внутренних углов выпуклого многоугольника.

Плоская фигура, образованная замкнутой цепочкой отрезков, называется многоугольником . В зависимости от количества углов многоугольник может быть треугольником , четырёхугольником , пятиугольником , шестиугольником и т.д. На рис.17 показан шестиугольник ABCDEF. Точки А, В, C, D, E, F – вершины

Многоугольника ; углы A , B , C , D, E , F – углы многоугольника ; отрезки AC, AD, BE и т.д. - диагонали ; AB, BC, CD, DE, EF, FA – стороны многоугольника ; сумма длин сторон AB + BC + … + FA называется периметром и обозначается p (иногда обозначают – 2p , тогда p – полупериметр ). В элементарной геометрии рассматриваются только простые многоугольники, контуры которых не имеют самопересечений, как показано на рис.18. Если все диагонали лежат внутри многоугольника, он называется выпуклым . Шестиугольник на рис.17 выпуклый; пятиугольник ABCDE на рис.19 не выпуклый, так как его диагональ AD лежит снаружи. Сумма внутренних углов выпуклого многоугольника равна 180º ( n – 2), где n - число углов (или сторон) многоугольника.

Параллелограмм. Свойства и признаки параллелограмма.

Прямоугольник. Основные свойства прямоугольника. Ромб.

Квадрат. Трапеция. Средние линии трапеции и треугольника.

Параллелограмм (ABCD, рис.32) – это четырёхугольник, противоположные стороны которого попарно параллельны.

Любые две противоположные стороны параллелограмма называются его основаниями , а расстояние между ними – высотой (BE, рис.32).

Свойства параллелограмма.

1. Противоположные стороны параллелограмма равны (AB = CD, AD = BC).

2. Противоположные углы параллелограмма равны ( A = C, B = D).

3. Диагонали параллелограмма делятся в точке их пересечения пополам (AO = OC, BO = OD).

4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон :

AC² + BD² = AB² + BC² + CD² + AD² .

Признаки параллелограмма.

Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:

1. Противоположные стороны попарно равны (AB = CD, AD = BC).

2. Противоположные углы попарно равны ( A = C, B = D).

3. Две противоположные стороны равны и параллельны (AB = CD, AB || CD).

4. Диагонали делятся в точке их пересечения пополам (AO = OC, BO = OD).

Прямоугольник.

Br />
Если один из углов параллелограмма прямой, то все остальные углы также прямые (почему?). Такой параллелограмм называется прямоугольником (рис.33) .

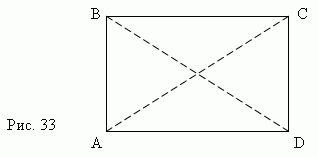
Основные свойства прямоугольника.

Стороны прямоугольника являются одновременно его высотами.

Диагонали прямоугольника равны: AC = BD.

Квадрат диагонали прямоугольника равен сумме квадратов его сторон (см. выше теорему Пифагора):

AC 2 = AD 2 + DC 2 .

Ромб. Если все стороны параллелограмма равны, то этот параллелограмм называется ромбом (рис.34) .

Диагонали ромба взаимно перпендикулярны (AC BD) и делят их углы пополам (DCA = BCA, ABD = CBD и т.д.).

Квадрат – это параллелограмм с прямыми углами и равными сторонами (рис.35). Квадрат является частным случаем прямоугольника и ромба одновременно; поэтому он обладает всеми их вышеперечисленными свойствами.

R />
Трапеция - это четырёхугольник, у которого е противоположные сто роны параллельны (рис.36).

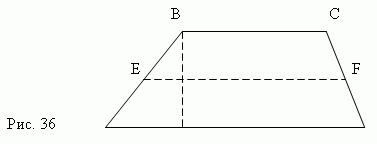
Здесь AD || BC. Параллельные стороны называются основаниями трапеции, а две другие (AB и CD) – боковыми сторонами. Расстояние между основаниями (BM) есть высота. Отрезок EF, соединяющий средние точки E и F

Боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований:

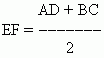
и параллельна им: EF || AD и EF || BC.

Трапеция с равными боковыми сторонами (AB = CD) называется равнобоч ной трапецией. В равнобочной трапеции углы при каждом основании равны ( A = D, B = C).

Параллелограмм может рассматриваться как частный случай трапеции.

Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине го основания и параллельна ему. о свойство вытекает из предыдущего

Пункта, так как треугольник может рассматриваться как случай вырождения трапеции, когда одно из её оснований превращается в точку.

Вписанный в круг многоугольник .

Описанный около круга многоугольник .

Описанный около многоугольника круг.

Вписанный в многоугольник круг.

Радиус вписанного в треугольник круга .

Радиус описанного около треугольника круга .
Правильный многоугольник.

Центр и апофема правильного многоугольника.
Соотношения сторон и радиусов правильных многоугольников .

Вписанным в круг называется многоугольник, вершины которого расположены на окружности рис.54). Описанным около круга называется ногоугольник, стороны которого являются касательными к окружности

(рис.55).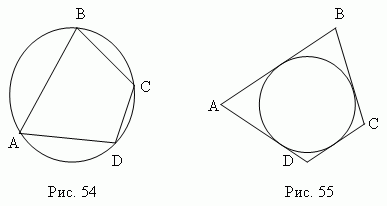

Соответственно, окружность, проходящая через вершины многоугольника (рис.54), называется описанной около многоугольника ; окружность, для которой стороны многоугольника являются касательными (рис.55) , на зывается вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность . Для треуголь ника это всегда возможно.

Радиус r вписанного круга выражается через стороны a, b, c треугольника:

Радиус R описанного круга выражается формулой: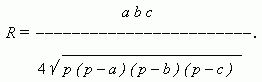

В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, еслитолько она равнобочная.r />

Правильный многоугольник то многоугольник с равными сторонами и углами.

На рис.56 показан правильный шестиугольник, а на рис.57 – правильный восьмиугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º (n – 2) / n ,где n – число его углов. Внутри правильного многоугольника существует точка O (рис. 56), равноудалённая от всех его вершин (OA = OB = OC = … = OF), которая называется центром правильного многоугольника. Центр правильного многоугольника также равноудалён от всех его сторон (OP = OQ = OR = …). Отрезки OP, OQ, OR, … называются апофемами ; отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный многоугольник можно вписать окружность и около него можно описать окружность. Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника. Радиус описанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема. Соотношения сторон и радиусов правильных многоугольников:

Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.

П р и м е р. Можно ли вырезать квадрат со стороной 30 см из круга

Диаметром 40 см?

Р е ш е н и е. Наибольший квадрат, заключённый в круг, есть вписанный

Квадрат. В соответствии с вышеприведенной формулой его

Сторона равна:

Следовательно, квадрат со стороной 30 см невозможно вырезать

Из круга диаметром 40 см.

Многоугольник - это геометрическая фигура, ограниченная замкнутой ломаной линией , не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника , а её вершины - вершинами многоугольника .

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью - пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A , B , C , D и E - это вершины пятиугольника, а отрезки AB , BC , CD , DE и EA - стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым , если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым :

Периметр

Сумма длин всех сторон многоугольника называется его периметром .

Периметр многоугольника ABCDE равен:

AB + BC + CD + DE + EA

Если у многоугольника равны все стороны и все углы, то его называют правильным . Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника - это отрезок , соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

t = n - 2

где t - это количество треугольников, а n - количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить .

Свойства многоугольников

Многоугольник - это геометрическая фигура, обычно определяется как замкнутая ломаная без самопересечений (простой многоугольник (рис. 1а)), однако иногда самопересечения допускаются (тогда многоугольник не является простым).

Вершины ломаной называются вершинами многоугольника, а отрезки - сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.

Углом (или внутренним углом) выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, при этом угол считается со стороны многоугольника. В частности угол может превосходить 180° если многоугольник невыпуклый.

Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разница между 180° и внутренним углом. Из каждой вершины -угольника при > 3 выходят - 3 диагонали, поэтому общее число диагоналей -угольника равно.

Многоугольник с тремя вершинами называется треугольником, с четырьмя - четырёхугольником, с пятью - пятиугольником и т.д.

Многоугольник с n вершинами называется n- угольником.

Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади.

Многоугольник называют выпуклым, если выполнено одно из следующих (эквивалентных) условий:

• 1. он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (т.е. продолжения сторон многоугольника не пересекают других его сторон);
• 2. он является пересечением (т.е. общей частью) нескольких полуплоскостей;
• 3. любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит.

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны, например равносторонний треугольник, квадрат и пентагон.

Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности

Правильный многоугольник - это многоугольник, у которого все углы и все стороны равны между собой.

Свойства многоугольников:

1 Каждая диагональ выпуклого -угольника, где >3, разлагает его на два выпуклых многоугольника.

2 Сумма всех углов выпуклого -угольника равна.

Д-во: Теорему докажем методом математической индукции. При = 3 она очевидна. Предположим, что теорема верна для -угольника, где <, и докажем ее для -угольника.

Пусть- данный многоугольник. Проведем диагональ этого многоугольника. По теореме 3 многоугольник разложен на треугольник и выпуклый -угольник (рис. 5). По предположению индукции. С другой стороны, . Складывая эти равенства и учитывая, что ( - внутренний луч угла ) и (- внутренний луч угла), получаем.При получаем: .

3 Около любого правильного многоугольника можно описать окружность, и притом только одну.

Д-во: Пусть правильный многоугольник, а и - биссектрисы углов, и (рис. 150). Так как, то, следовательно, * 180° < 180°. Отсюда следует, что биссектрисы и углов и пересекаются в некоторой точке О. Докажем, что O = ОА 2 = О =… = ОА п . Треугольник О равнобедренный, поэтому О = О . По второму признаку равенства треугольников, следовательно, О = О . Аналогично доказывается, что О = О и т.д. Таким образом, точка О равноудалена от всех вершин многоугольника, поэтому окружность с центром О радиуса О является описанной около многоугольника.

Докажем теперь, что описанная окружность только одна. Рассмотрим какие-нибудь три вершины многоугольника, например, А 2 , . Так как через эти точки проходит только одна окружность, то около многоугольника… нельзя описать более чем одну окружность.

• 4 В любой правильный многоугольник можно вписать окружность и притом только одну.
• 5 Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
• 6 Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
• 7 Симметрия:

Говорят, что фигура обладает симметрией (симметрична), если существует такое движение (не тождественное), переводящее эту фигуру в себя.

• 7.1. Треугольник общего вида не имеет осей или центров симметрии, он несимметричен. Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии: серединный перпендикуляр к основанию.
• 7.2. Равносторонний треугольник имеет три оси симметрии (серединные перпендикуляры к сторонам) и поворотную симметрию относительно центра с углом поворота 120°.

7.3 У любого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он также имеет поворотную симметрию относительно центра с углом поворота.

При четном n одни оси симметрии проходят через противоположные вершины, другие - через середины противоположных сторон.

При нечетном n каждая ось проходит через вершину и середину противоположной стороны.

Центр правильного многоугольника с четным числом сторон является его центром симметрии. У правильного многоугольника с нечетным числом сторон центра симметрии нет.

8 Подобие:

При подобии и -угольник переходит в -угольник, полуплоскость - в полуплоскость, поэтому выпуклый n -угольник переходит в выпуклый n -угольник.

Теорема: Если стороны и углы выпуклых многоугольников иудовлетворяют равенствам:

где - коэффициент подия

то эти многоугольники подобны.

• 8.1 Отношение периметров двух подобных многоугольников равно коэффициенту подобия.
• 8.2. Отношение площадей двух выпуклых подобных многоугольников равно квадрату коэффициента подобия.

многоугольник треугольник периметр теорема

Существуют разные точки зрения на то, что считать многоугольником. В школьном курсе геометрии используют одно из следующих определений.

Определение 1

Многоугольник

— это фигура, составленная из отрезков

так, что смежные отрезки (то есть соседние отрезки с общей вершиной, например, A1A2 и A2A3) не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

Определение 2

Многоугольником называется простая замкнутая .

Точки

называются вершинами многоугольника , отрезки

— сторонами многоугольника .

Сумма длин всех сторон называется периметром многоугольника .

Многоугольник, который имеет n вершин (а значит, и n сторон) называется n — угольником .

Многоугольник, который лежит в одной плоскости, называется плоским . Когда говорят о многоугольнике, если не сказано иначе, подразумевается, что речь идёт о плоском многоугольнике.

Две вершины, принадлежащие одной стороне многоугольника, называются соседними . Например, A1 и A2, A5 и A6 — соседние вершины.

Отрезок, который соединяет две несоседние вершины, называется диагональю многоугольника .

Выясним, сколько диагоналей имеет многоугольник.

Из каждой из n вершин многоугольника исходит n-3 диагонали

(всего вершин n. Не считаем саму вершину и две соседние, которые не образуют с данной вершиной диагонали. Для вершины A1, например, не учитываем саму A1 и соседние вершины A2 и A3).

Таким образом, каждой из n вершин соответствует n-3 диагонали. Поскольку одна диагональ относится сразу к двум вершинам, чтобы найти количество диагоналей многоугольника, надо произведение n(n-3) разделить пополам.

Следовательно, n — угольник имеет

диагонали.

Любой многоугольник делит плоскость на две части — внутреннюю и внешнюю области многоугольника. Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником.